単純平均値
対象となるデータ(変数)について1行(1つ)ずつすべての値を合計して、データの個数(行数)で割り算した値。
式で表すと次のようになります。
次のどちらも同じ意味です。
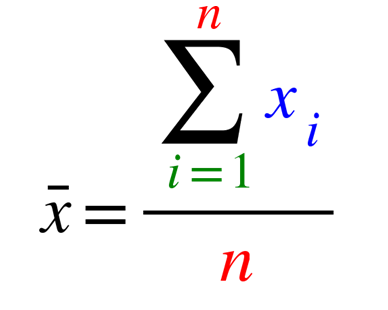
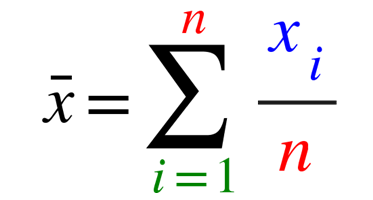
すなわち次の式で表わすこともできます。
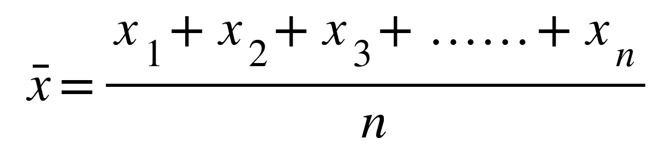
「![]() 」は「エックスバー」と読み、データの平均値を意味します。
」は「エックスバー」と読み、データの平均値を意味します。
平均値は必ずしも多勢を表わす指標ではないことに注意が必要です。
なお他にも平均値と呼ぶ指標があり、それ特別するため、単純平均値(たんじゅんへいきんち)、相加平均値(そうかへいきんち)と表わすことがあります。
ExcelではAVERAGE関数で求めることができます。
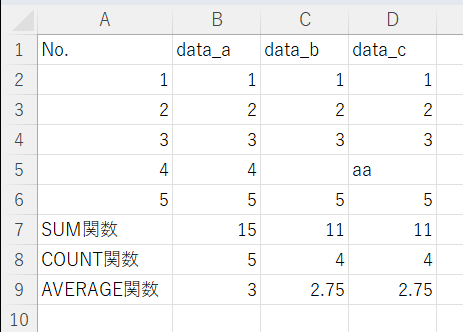
範囲指定した中に空白や文字列のセルが含まれると、データ個数にはカウントされず、無視されます。
この場合は合計がが15、空白セルや文字列を含む5つのセルを範囲選択したら、データ個数は4とカウントされ、単純平均値は 11 ÷ 4 = 2.75と出力されます。
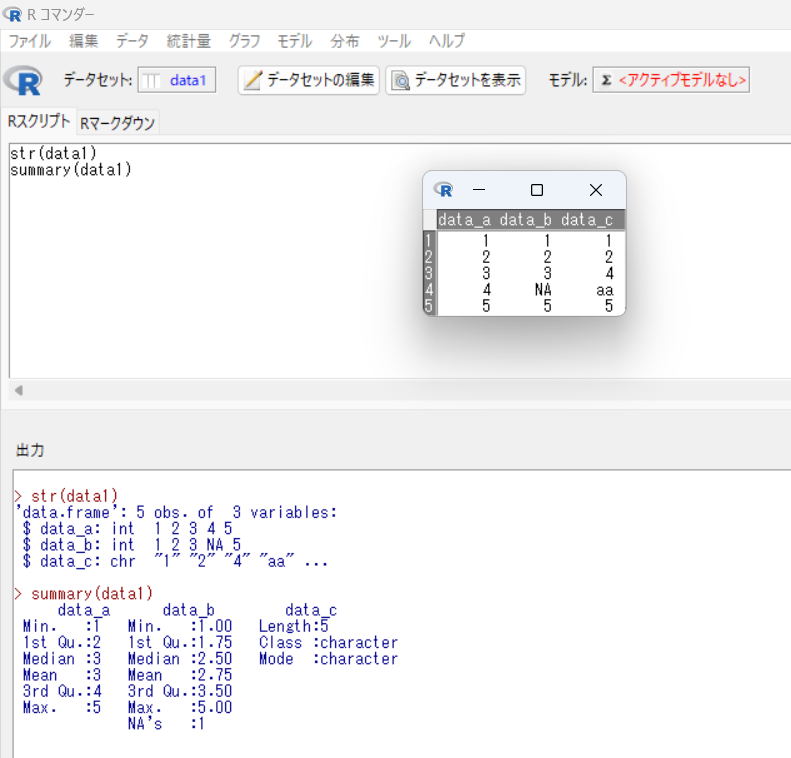
Rの場合、平均値(mean)はdata_aが3、data_bが2.75と表示されています。
文字列を含む列(ここではdata_c)では、文字列のデータとして認識されています。
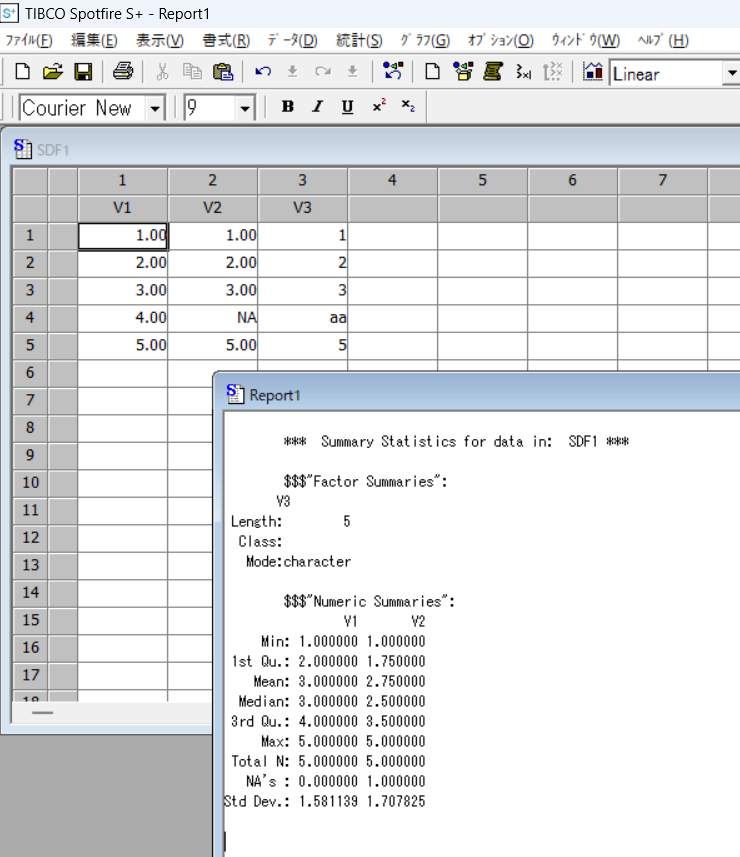
S-PLUSではdata_cは文字列(Data Typeを「character」とする)にしないと「aa」と入力・認識できません。
その上で、data_aは平均値が3、data_bは平均値が2.75と表示されました。
度数分布表からおおよその平均値を求める
度数分布表を基に場合は、「階級値」と「度数」から、おおよその平均値を求める方法があります。
| 階級(身長の場合) | 階級値 | 度数 |
|---|---|---|
| 130cm以上140cm未満 | 135cm | 2 |
| 140cm以上 150cm未満 | 145cm | 6 |
| 150cm以上 160cm未満 | 155cm | 8 |
| 160cm以上 170cm未満 | 165cm | 4 |
| 170cm以上 180cm未満 | 175cm | 2 |
130cm以上 140cm未満の階級に2人が含まれる場合……
- 階級値(かいきゅうち)を135cmとします。
- 130cm以上 140cm未満の階級が2人なので、135 × 2を計算します。
- この要領で140cm以上 150cm未満の階級についても計算をします(145 × 6)。
- 150cm以上160cm未満の階級(155 × 8)、160~170cm(165 × 4)、170~180cm(175 × 2)と計算をし、すべて合計します(135 × 2 + 145 × 6 + 155 × 8 + 165 × 4 + 175 × 2 = 3,390)
- 全体の度数(つまり全体の人数)で割り算したものを、度数分布表から平均値とします
(3,390 ÷ 22 ≒ 154.09)。